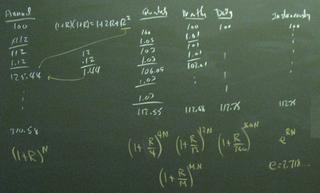January 16, 2003
Interest Rates
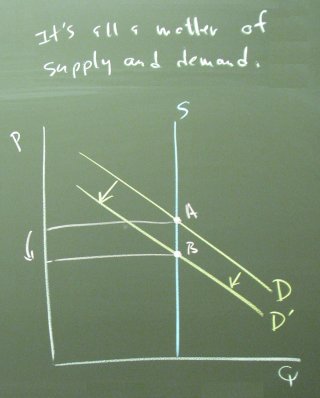We began the discussion of financial markets today with an explanation for yesterday's decline in the stock market. While the WSJ attributed the outcome to unfavorable earnings reports, we were able to explain the phenomenon with our usual diagram, modifed slightly to account for the fixed supply of shares of stock.
Similiar diagrams will allow us to explain ex post the stock market movements for the rest of the semester. These explanation, while certainly true, will lack a certain depth. Consequently, we moved on to a more objective methodology for valuing financial assets.
There are two basic forces at work determining the values of financial assets. These are competition among similar assets and the potential for arbitrage profits. An arbitrage profit has two elements. (i) It is risk-free. (ii) You do not put up any of your own money.
There are two essential elements to a scientific study of a new discovery. (1) Name it. (2) Measure it. The financial assets all have names. We are trying to formulate a way to measure them. Our yardstick will be a risk-free bank account.
We looked in some detail at the forces determining the price today of a bond that will pay $1000 next year.
Arbitrage pricing tells us that, if the interest rate is 10%, then a bond that pays $1000 next year will be worth $909.09 right now. Otherwise, there will be a way to collect arbitrage profits. We are assuming here that the bond is risk-free and that agents can borrow and lend unlimited amounts at 10%. (The arbitrage-free equilibrium is on the far right. The upper calculations show arbitrage profits next year. The lower calculations show arbitrage profits now.)
If we are going to use interest rates to value financial assets, then we to develop our skills with interest rate calculations. We studied the table below, which is also a handout. If you missed class: handouts in a pdf file. There are some pages included that will be distributed in future class meetings.
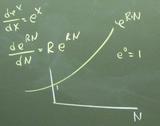
The exponential function is the only function that is its own first derivative. This means that exp(RN) grows at the rate R exp(RN). In words, a bank balance grows in proportion to how big it already is. On the right, any number raised to the zero power equals one.